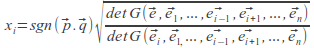Обратни матрици на произволни.

В линейната алгебра на всяка квадратна матрица A може да се дефинира нейната обратна A^-1 ( при det A ≠ 0 ), като A A^-1 = A^-1A= E , където E е единичната матрица. Ако за матрицата A имаме

 

то също можем да дефинираме обратна матрица на А. Да я означим с L_1. Тогава,

със свойството:

 и

 

ще наричаме обратна матрица на А.

Обратната матрица L₁ на A вече няма да е еднозначно определена. Те вече ще образуват множество L от обратните матрици на А. т.е.

Да разгледаме частният случай 

 

Тогава търсим матрица L₁ със свойствата:

 

Нека:

 и  

 

 

От системата:

получаваме следната система от 13 уравнения с 6 неизвестни.

 

a₁₁x₁₁ + a₁₂x₂₁ + a₁₃x₃₁ = 1
a₁₁x₁₂ + a₁₂x₂₂ + a₁₃x₃₂ = 0
a₂₁x₁₁ + a₂₂x₂₁ + a₂₃x₃₁ = 0
a₂₁x₁₂ + a₂₂x₂₂ + a₂₃x₃₂ = 1


a₁₁x₁₁ + a₂₁x₁₂ = 1
a₁₂x₁₁ + a₂₂x₁₂ = 0
a₁₃x₁₁ + a₂₃x₁₂ = 0
a₁₁x₂₁ + a₂₁x₂₂ = 0
a₁₂x₂₁ + a₂₂x₂₂ = 0
a₁₃x₂₁ + a₂₃x₂₂ = 0
a₁₁x₃₁ + a₂₁x₃₂ = 0
a₁₂x₃₁ + a₂₂x₃₂ = 0
a₁₃x₃₁ + a₂₃x₃₂ = 1

 

Но за такива системи линейни уравнения (свръхопределени), вече имаме явна формула Обобщена формула на Крамер (Cramer's rule) :

В системата с 13 уравнения полагаме x₁ = x₁₁, x₂ = x₁₂, x₃ = x₂₁, x₄ = x₂₂, x₅ = x₃₁, x₆ = x₃₂. Да означим с e₁, e₂, e₃, e₄, e₅, e₆, e – вектор-стълбовете на така получената матрица. Тогава едната обратна матрица на А е:

 като:

Продължение на "Една формула с функцията цяла част."

където k принадлежи на N (множеството на натуралните числа).

Една формула с функцията цяла част.

Може да се докаже, като се разгледат случаите за n четно и нечетно.