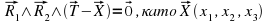1. "Килим" на Серпински.
вторник, 23 февруари 2010 г.
неделя, 21 февруари 2010 г.
неделя, 7 февруари 2010 г.
Уравнение на равнина във векторен вид.
Това е едно приложение на обобщеното векторно произведение, което е изложено в:
Векторно произведение в n – мерният случай.
Първо ще разгледаме случая в тримерното пространство.
Нека имаме правите l1, l2 и равнина L, като .
.
Нека правите l1, l2 са определени чрез векторите:

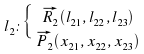
Нека T ( t1, t2, t3 ) е произволна точка от L. Тогава, за да може произволна точка X (x1, x2, x3) също да принадлежи на L трябва да е в сила:
което е векторното уравнение на равнината L в тримерното пространство.
Всяка равнина в тримерното пространство се определя от 2 вектора и една точка. Така че, ако
 то уравнението може да се запише така:
то уравнението може да се запише така:
В общият случай: Rn искаме да определим P подпространство на Rn, като dim P = n-1, чрез векторите R1, R2, ... , Rn-1 и точка T от Rn, като T (t1', ... , tn'). Тогава векторното уравнение на P е:
Ще отбележа само, че в пространство Rn векторното произведение е определено не само за n-1 на брой вектори от Rn, но и за n на брой вектора от Rn. Така че горните формули са напълно коректни.
Векторно произведение в n – мерният случай.
Първо ще разгледаме случая в тримерното пространство.
Нека имаме правите l1, l2 и равнина L, като
 .
.Нека правите l1, l2 са определени чрез векторите:

и
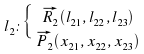
Нека T ( t1, t2, t3 ) е произволна точка от L. Тогава, за да може произволна точка X (x1, x2, x3) също да принадлежи на L трябва да е в сила:
което е векторното уравнение на равнината L в тримерното пространство.
Всяка равнина в тримерното пространство се определя от 2 вектора и една точка. Така че, ако

Абонамент за:
Публикации (Atom)