Векторно произведение в n – мерният случай.
Първо ще разгледаме случая в тримерното пространство.
Нека имаме правите l1, l2 и равнина L, като
 .
.Нека правите l1, l2 са определени чрез векторите:

и
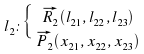
Нека T ( t1, t2, t3 ) е произволна точка от L. Тогава, за да може произволна точка X (x1, x2, x3) също да принадлежи на L трябва да е в сила:
което е векторното уравнение на равнината L в тримерното пространство.
Всяка равнина в тримерното пространство се определя от 2 вектора и една точка. Така че, ако


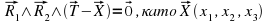
Няма коментари:
Публикуване на коментар