сряда, 17 ноември 2010 г.
понеделник, 24 май 2010 г.
вторник, 11 май 2010 г.
Сайт с java аплети свързани с математиката.
http://www.jinnee.info/ е сайт с java аплети свързани с математиката. На него можете да видите някои фрактали. По нататък ще реализирам и други алгоритми свързани с математиката. За да разгледате сайта ще трябва да имате инсталирана java. Приятно забавление :-)
сряда, 7 април 2010 г.
Стойности на функцията на Ойлер.
Стойности на функцията на Ойлер φ(n) ( Euler's totient function). Файлът е компресиран zip.
Може да се свали от тук.
Може да се свали от тук.
сряда, 31 март 2010 г.
Списък с признаци за деление на първите 200 прости числа.
Признаци за делимост на прости числа (prime number). без 2 и 5.
Продължение на:
Примери за признаци за делимост на някои прости числа (prime numbers).
3|a1a2 ... an-1 + 1.an
7|a1a2 ... an-1 + 5.an
11|a1a2 ... an-1 + 10.an
13|a1a2 ... an-1 + 4.an
17|a1a2 ... an-1 + 12.an
19|a1a2 ... an-1 + 2.an
23|a1a2 ... an-1 + 7.an
29|a1a2 ... an-1 + 3.an
31|a1a2 ... an-1 + 28.an
37|a1a2 ... an-1 + 26.an
Продължение на:
Примери за признаци за делимост на някои прости числа (prime numbers).
3|a1a2 ... an-1 + 1.an
7|a1a2 ... an-1 + 5.an
11|a1a2 ... an-1 + 10.an
13|a1a2 ... an-1 + 4.an
17|a1a2 ... an-1 + 12.an
19|a1a2 ... an-1 + 2.an
23|a1a2 ... an-1 + 7.an
29|a1a2 ... an-1 + 3.an
31|a1a2 ... an-1 + 28.an
37|a1a2 ... an-1 + 26.an
сряда, 24 март 2010 г.
Едно свойство на клас прости числа.
Нека p е просто число (prime number) като 64 | p-1,
тогава p може да се представи като сума на три квадрата.
Примери:
193 = 112+62+62
257 = 152+42+42
449 = 212+22+22
577 = 212+102+62
641 = 242+82+12
769 = 242+122+72
и т.н.
Изведено е чрез теория на решетките.
тогава p може да се представи като сума на три квадрата.
Примери:
193 = 112+62+62
257 = 152+42+42
449 = 212+22+22
577 = 212+102+62
641 = 242+82+12
769 = 242+122+72
и т.н.
Изведено е чрез теория на решетките.
неделя, 14 март 2010 г.
Алгоритъм за коренуване.
„Бог е създал целите числа, всичко останало е човешко дело“ Леополд Кронекер.
Следващият алгоритъм който ще изложа се може да се използва за изчисляване стойността на натурални числа повдигнати на степен рационално число т.е. казвам може, защото алгоритъмът е трудоемък (може би и поради това не съм го срещал :-), но въпреки това е много интересен. Той дава възможност да се види редът в:
21/2 = 1,4142135623730950488016887242096980785
6967187537694807317667973799073247846210703
8850387534327641572735013846230912297024924
8360558507372126441214970999358314132226659
2750559275579995050115278206057147...
изчислено именно по този алгоритъм (разбира се с компютър :-)
Обикновено са ни казвали, че при ирационалните числа няма периодичност на цифрите след десетичната запетая, но ... това не означава, че няма закон за появата на тези цифри. На пръв поглед няма някаква зависимост при цифрите след десетичната запетая в 21/2.
Да разгледаме следната задача:
Задача: Да се намери редица от естествени числа:
n1,n2, ... , nk, ... , k = 0, 1, 2, ... :
2*102k - nk*nk > 0 е минимално.
Не е трудно да намерим първите членове на тази редица:
за к = 0 имаме n0=1
за к = 1 имаме n1=14
за к = 2 имаме n2=141
за к = 3 имаме n3=1414
за к = 4 имаме n4=14142
и т.н.
Вижда се, че търсената редица съдържа числата на 21/2, което не трудно да се докаже, както и да се намери алгоритъм за общият случай.
Алгоритъмът е трудоемък, защото при всяка следваща стъпка имаме умножение на все по-големи числа. Но има предимството, че лесно се помни и трудността на изчисление не е голяма за първите 2-3 цифри след десетичната запетая.
Следващият алгоритъм който ще изложа се може да се използва за изчисляване стойността на натурални числа повдигнати на степен рационално число т.е. казвам може, защото алгоритъмът е трудоемък (може би и поради това не съм го срещал :-), но въпреки това е много интересен. Той дава възможност да се види редът в:
21/2 = 1,4142135623730950488016887242096980785
6967187537694807317667973799073247846210703
8850387534327641572735013846230912297024924
8360558507372126441214970999358314132226659
2750559275579995050115278206057147...
изчислено именно по този алгоритъм (разбира се с компютър :-)
Обикновено са ни казвали, че при ирационалните числа няма периодичност на цифрите след десетичната запетая, но ... това не означава, че няма закон за появата на тези цифри. На пръв поглед няма някаква зависимост при цифрите след десетичната запетая в 21/2.
Да разгледаме следната задача:
Задача: Да се намери редица от естествени числа:
n1,n2, ... , nk, ... , k = 0, 1, 2, ... :
2*102k - nk*nk > 0 е минимално.
Не е трудно да намерим първите членове на тази редица:
за к = 0 имаме n0=1
за к = 1 имаме n1=14
за к = 2 имаме n2=141
за к = 3 имаме n3=1414
за к = 4 имаме n4=14142
и т.н.
Вижда се, че търсената редица съдържа числата на 21/2, което не трудно да се докаже, както и да се намери алгоритъм за общият случай.
Алгоритъмът е трудоемък, защото при всяка следваща стъпка имаме умножение на все по-големи числа. Но има предимството, че лесно се помни и трудността на изчисление не е голяма за първите 2-3 цифри след десетичната запетая.
петък, 5 март 2010 г.
Деление на 7
Нека Аn = (111111)n777777777 за n = 1, 2, 3, ...., n, ..... Например: А1 = 111111777777777, А2 = 111111111111777777777 и т.н. Тогава 7 | Аn за n = 1, 2, 3, ...., n, .....Може да се докаже от признака за делимост на 7 .
вторник, 23 февруари 2010 г.
неделя, 21 февруари 2010 г.
неделя, 7 февруари 2010 г.
Уравнение на равнина във векторен вид.
Това е едно приложение на обобщеното векторно произведение, което е изложено в:
Векторно произведение в n – мерният случай.
Първо ще разгледаме случая в тримерното пространство.
Нека имаме правите l1, l2 и равнина L, като .
.
Нека правите l1, l2 са определени чрез векторите:

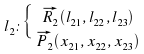
Нека T ( t1, t2, t3 ) е произволна точка от L. Тогава, за да може произволна точка X (x1, x2, x3) също да принадлежи на L трябва да е в сила:
което е векторното уравнение на равнината L в тримерното пространство.
Всяка равнина в тримерното пространство се определя от 2 вектора и една точка. Така че, ако
 то уравнението може да се запише така:
то уравнението може да се запише така:
В общият случай: Rn искаме да определим P подпространство на Rn, като dim P = n-1, чрез векторите R1, R2, ... , Rn-1 и точка T от Rn, като T (t1', ... , tn'). Тогава векторното уравнение на P е:
Ще отбележа само, че в пространство Rn векторното произведение е определено не само за n-1 на брой вектори от Rn, но и за n на брой вектора от Rn. Така че горните формули са напълно коректни.
Векторно произведение в n – мерният случай.
Първо ще разгледаме случая в тримерното пространство.
Нека имаме правите l1, l2 и равнина L, като
 .
.Нека правите l1, l2 са определени чрез векторите:

и
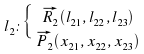
Нека T ( t1, t2, t3 ) е произволна точка от L. Тогава, за да може произволна точка X (x1, x2, x3) също да принадлежи на L трябва да е в сила:
което е векторното уравнение на равнината L в тримерното пространство.
Всяка равнина в тримерното пространство се определя от 2 вектора и една точка. Така че, ако

вторник, 26 януари 2010 г.
Умножение без частични произведения.
Ще изложа метод описан в книгата: "Математическа мозайка" изд. "Техника", която представлява сборник статии по математика на унгарски математици. Авторът споменава, че този метод е отдавна известен, но преоткрит от Феррол - "изчислителят-фокусник" живял в началото на миналия век. Този метод е особено подходящ за компютърна реализация и след като се помъча да го изложа ще дам негова реализация. Да разгледаме произведението 724 * 586. Обръщаме вторият множител и прилагаме следните стъпки:

Като стрелката изразява умножение на съответните цифри, като след умножението като резултат записваме цифрата на единиците, а тази на десетиците преминава като "едно наум" и се прибавя към следващото умножение. Например при първата стъпка имаме 6.4 = 24 - записваме 4 и 2 "наум". После пресмятаме 6.2+8.4+2 = 46 - пишем 6 и 4 "наум". Така продължаваме до края и получаваме търсеният резултат 424264.
А ето и реализацията на метода на c++ По-точно за компилатора g++.
Реализация на метода

Като стрелката изразява умножение на съответните цифри, като след умножението като резултат записваме цифрата на единиците, а тази на десетиците преминава като "едно наум" и се прибавя към следващото умножение. Например при първата стъпка имаме 6.4 = 24 - записваме 4 и 2 "наум". После пресмятаме 6.2+8.4+2 = 46 - пишем 6 и 4 "наум". Така продължаваме до края и получаваме търсеният резултат 424264.
А ето и реализацията на метода на c++ По-точно за компилатора g++.
Реализация на метода
понеделник, 25 януари 2010 г.
петък, 22 януари 2010 г.
Абонамент за:
Публикации (Atom)