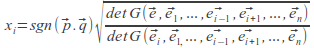Камий Жордан

Жордан, Камий, роден на 5 януари 1838 г. в Лион, починал на 20 или 21 януари 1922 г. в Милано. Следва в Париж и от 1960 г. е инженер в мините на Прива. От 1876 г. е професор в Екол Политехник. Работите му съдържат основни приноси към теория на групите, топологията и анализа.

"Математически енциклопедичен речник" Гелерт и др.

По - подробна биография на английски: Camille Jordan.

В Wikipedia:
Прива , Екол Политехник , Топология    

Обобщена синусова теорема за тетраедър. Приложение на векторното произведение.

Нека имаме векторите:

Разглеждаме хипервекторите:

 

Тогава:

 

където:

 

Но от друга страна имаме:

 

като под

 

разбираме представителите на

 

 

Тогава смесените произведения

 

са равни на 0. Така получаваме:

 

Но знаем, че

 

където h е дължината на перпендикуляра спуснат от края на

чрез преобразувания получаваме:

Окончателно:

Синусова теорема за тетраедър (сферичен триъгълник). Приложение на векторното произведение.

Дефиниция: 

Нека имаме хипервекторите

, тогава под векторно произведение на

ще разбираме векторното произведение на техните представители.

Нека имаме векторите:

 



като:

 Означаваме:

  

Нека имаме  хипервекторите:

 Тогава:

Извеждането на формулата за n-мерният случай е аналогично. В следващ пост ще бъде изложено и нейното доказателсво.

Косинусова теорема за тетраедър (сферичен триъгълник). Приложение на векторното произведение.

Нека имаме векторите:

 като

Означаваме:

Нека имаме хипервекторите  определени по следният начин:

Означаваме:

 

 

 Прилагаме дефиницията за скаларно произведение за хипервектори:

  

което представлява и косинусовата теорема за страните на сферичен триъгълник.

По аналогичен начин може да изведе и косинусовата теорема за n-мерна сфера.

Скаларно произведение на групи от вектори.

След представянето на векторното произведение за n-мерни вектори, ще разгледаме и скаларното произведение.

Дефиниция: n - мерен хипервектор ще наричаме всеки паралелепипед определен чрез наредената n – торка вектори . Представител на P ще наричаме вектора . Посоката на P се определя от p.

Дефиниция: Нека имаме хипервекторите , тогава ъгъл между хипервекторите P и Q ще наричаме ъгъла между техните представители.

Дефиниция: Нека имаме хипервекторите , тогава под скаларно произведение на P и Q ще разбираме скаларното произведение на техните представители.

Нека имаме хипервектора , като








Разглеждаме детерминантите:

образувани от векторите на P. Тези детерминанти ще ги означаваме с гръцки букви и ще ги наричаме координати на хипервектора P.

Тогава . . Вече показахме, че .

От вече доказаната формула:



, можем да получим и формулата

Обратни матрици на произволни.

В линейната алгебра на всяка квадратна матрица A може да се дефинира нейната обратна A^-1 ( при det A ≠ 0 ), като A A^-1 = A^-1A= E , където E е единичната матрица. Ако за матрицата A имаме

 

то също можем да дефинираме обратна матрица на А. Да я означим с L_1. Тогава,

със свойството:

 и

 

ще наричаме обратна матрица на А.

Обратната матрица L₁ на A вече няма да е еднозначно определена. Те вече ще образуват множество L от обратните матрици на А. т.е.

Да разгледаме частният случай 

 

Тогава търсим матрица L₁ със свойствата:

 

Нека:

 и  

 

 

От системата:

получаваме следната система от 13 уравнения с 6 неизвестни.

 

a₁₁x₁₁ + a₁₂x₂₁ + a₁₃x₃₁ = 1
a₁₁x₁₂ + a₁₂x₂₂ + a₁₃x₃₂ = 0
a₂₁x₁₁ + a₂₂x₂₁ + a₂₃x₃₁ = 0
a₂₁x₁₂ + a₂₂x₂₂ + a₂₃x₃₂ = 1


a₁₁x₁₁ + a₂₁x₁₂ = 1
a₁₂x₁₁ + a₂₂x₁₂ = 0
a₁₃x₁₁ + a₂₃x₁₂ = 0
a₁₁x₂₁ + a₂₁x₂₂ = 0
a₁₂x₂₁ + a₂₂x₂₂ = 0
a₁₃x₂₁ + a₂₃x₂₂ = 0
a₁₁x₃₁ + a₂₁x₃₂ = 0
a₁₂x₃₁ + a₂₂x₃₂ = 0
a₁₃x₃₁ + a₂₃x₃₂ = 1

 

Но за такива системи линейни уравнения (свръхопределени), вече имаме явна формула Обобщена формула на Крамер (Cramer's rule) :

В системата с 13 уравнения полагаме x₁ = x₁₁, x₂ = x₁₂, x₃ = x₂₁, x₄ = x₂₂, x₅ = x₃₁, x₆ = x₃₂. Да означим с e₁, e₂, e₃, e₄, e₅, e₆, e – вектор-стълбовете на така получената матрица. Тогава едната обратна матрица на А е:

 като: